更新公示编译后无法正常现实的问题

docs/ml/14.利用SVD简化数据.md

@@ -47,12 +47,12 @@
 > SVD 是矩阵分解的一种类型，也是矩阵分解最常见的技术
 
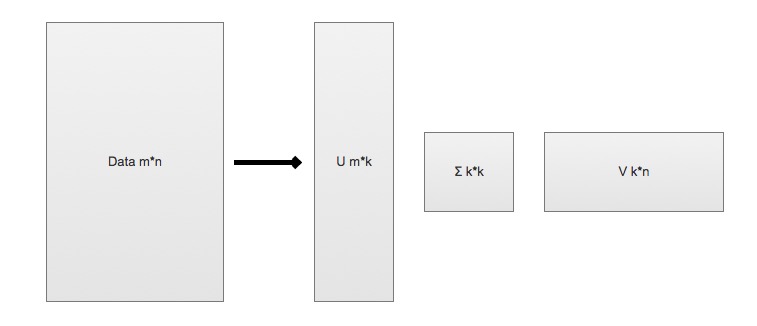
 * SVD 将原始的数据集矩阵 Data 分解成三个矩阵 U、∑、V
-* 举例: 如果原始矩阵 \\(Data_{m*n}\\) 是m行n列，
-    * \\(U_{m * k}\\) 表示m行k列
-    * \\(∑_{k * k}\\) 表示k行k列
-    * \\(V_{k * n}\\) 表示k行n列。
+* 举例: 如果原始矩阵 $$Data_{m*n}$$ 是m行n列，
+    * $$U_{m * k}$$ 表示m行k列
+    * $$∑_{k * k}$$ 表示k行k列
+    * $$V_{k * n}$$ 表示k行n列。
     
-\\(Data_{m*n} = U_{m\*k} \* ∑_{k\*k} \* V_{k\*n}\\)
+$$Data_{m*n} = U_{m\*k} \* ∑_{k\*k} \* V_{k\*n}$$
 
 ![SVD公式](http://data.apachecn.org/img/AiLearning/ml/14.SVD/使用SVD简化数据-SVD公式.jpg)
 
@@ -61,7 +61,7 @@
 ![SVD公式](http://data.apachecn.org/img/AiLearning/ml/14.SVD/SVD公式的测试案例.jpg)
 
 * 上述分解中会构建出一个矩阵∑，该矩阵只有对角元素，其他元素均为0(近似于0)。另一个惯例就是，∑的对角元素是从大到小排列的。这些对角元素称为奇异值。
-* 奇异值与特征值(PCA 数据中重要特征)是有关系的。这里的奇异值就是矩阵 \\(Data * Data^T\\) 特征值的平方根。
+* 奇异值与特征值(PCA 数据中重要特征)是有关系的。这里的奇异值就是矩阵 $$Data * Data^T$$ 特征值的平方根。
 * 普遍的事实: 在某个奇异值的数目(r 个=>奇异值的平方和累加到总值的90%以上)之后，其他的奇异值都置为0(近似于0)。这意味着数据集中仅有 r 个重要特征，而其余特征则都是噪声或冗余特征。
 
 ### SVD 算法特点

docs/ml/6.支持向量机.md

@@ -61,44 +61,44 @@ Support Vector Machines: Slide 12 Copyright © 2001, 2003, Andrew W. Moore Why M
 
 > 点到超平面的距离
 
-* 分隔超平面`函数间距`:  \\(y(x)=w^Tx+b\\)
-* 分类的结果:  \\(f(x)=sign(w^Tx+b)\\)  (sign表示>0为1，<0为-1，=0为0) 
-* 点到超平面的`几何间距`: \\(d(x)=(w^Tx+b)/||w||\\)  （||w||表示w矩阵的二范数=> \\(\sqrt{w^T*w}\\), 点到超平面的距离也是类似的）
+* 分隔超平面`函数间距`:  $$y(x)=w^Tx+b$$
+* 分类的结果:  $$f(x)=sign(w^Tx+b)$$  (sign表示>0为1，<0为-1，=0为0) 
+* 点到超平面的`几何间距`: $$d(x)=(w^Tx+b)/||w||$$  （||w||表示w矩阵的二范数=> $$\sqrt{w^T*w}$$, 点到超平面的距离也是类似的）
 
 ![点到直线的几何距离](http://data.apachecn.org/img/AiLearning/ml/6.SVM/SVM_4_point2line-distance.jpg)
 
 > 拉格朗日乘子法
 
-* 类别标签用-1、1，是为了后期方便 \\(label*(w^Tx+b)\\) 的标识和距离计算；如果 \\(label*(w^Tx+b)>0\\) 表示预测正确，否则预测错误。
+* 类别标签用-1、1，是为了后期方便 $$label*(w^Tx+b)$$ 的标识和距离计算；如果 $$label*(w^Tx+b)>0$$ 表示预测正确，否则预测错误。
 * 现在目标很明确，就是要找到`w`和`b`，因此我们必须要找到最小间隔的数据点，也就是前面所说的`支持向量`。
     * 也就说，让最小的距离取最大.(最小的距离: 就是最小间隔的数据点；最大: 就是最大间距，为了找出最优超平面--最终就是支持向量)
-    * 目标函数: \\(arg: max_{关于w, b} \left( min[label*(w^Tx+b)]*\frac{1}{||w||} \right) \\)
-        1. 如果 \\(label*(w^Tx+b)>0\\) 表示预测正确，也称`函数间隔`，\\(||w||\\) 可以理解为归一化，也称`几何间隔`。
-        2. 令 \\(label*(w^Tx+b)>=1\\)， 因为0～1之间，得到的点是存在误判的可能性，所以要保障 \\(min[label*(w^Tx+b)]=1\\)，才能更好降低噪音数据影响。
-        3. 所以本质上是求 \\(arg: max_{关于w, b}  \frac{1}{||w||} \\)；也就说，我们约束(前提)条件是: \\(label*(w^Tx+b)=1\\)
-* 新的目标函数求解:  \\(arg: max_{关于w, b}  \frac{1}{||w||} \\)
-    * => 就是求: \\(arg: min_{关于w, b} ||w|| \\) (求矩阵会比较麻烦，如果x只是 \\(\frac{1}{2}*x^2\\) 的偏导数，那么。。同样是求最小值)
-    * => 就是求: \\(arg: min_{关于w, b} (\frac{1}{2}*||w||^2)\\) (二次函数求导，求极值，平方也方便计算)
+    * 目标函数: $$arg: max_{关于w, b} \left( min[label*(w^Tx+b)]*\frac{1}{||w||} \right) $$
+        1. 如果 $$label*(w^Tx+b)>0$$ 表示预测正确，也称`函数间隔`，$$||w||$$ 可以理解为归一化，也称`几何间隔`。
+        2. 令 $$label*(w^Tx+b)>=1$$， 因为0～1之间，得到的点是存在误判的可能性，所以要保障 $$min[label*(w^Tx+b)]=1$$，才能更好降低噪音数据影响。
+        3. 所以本质上是求 $$arg: max_{关于w, b}  \frac{1}{||w||} $$；也就说，我们约束(前提)条件是: $$label*(w^Tx+b)=1$$
+* 新的目标函数求解:  $$arg: max_{关于w, b}  \frac{1}{||w||} $$
+    * => 就是求: $$arg: min_{关于w, b} ||w|| $$ (求矩阵会比较麻烦，如果x只是 $$\frac{1}{2}*x^2$$ 的偏导数，那么。。同样是求最小值)
+    * => 就是求: $$arg: min_{关于w, b} (\frac{1}{2}*||w||^2)$$ (二次函数求导，求极值，平方也方便计算)
     * 本质上就是求线性不等式的二次优化问题(求分隔超平面，等价于求解相应的凸二次规划问题)
 * 通过拉格朗日乘子法，求二次优化问题
     * 假设需要求极值的目标函数 (objective function) 为 f(x,y)，限制条件为 φ(x,y)=M  # M=1
-    * 设g(x,y)=M-φ(x,y)   # 临时φ(x,y)表示下文中 \\(label*(w^Tx+b)\\)
+    * 设g(x,y)=M-φ(x,y)   # 临时φ(x,y)表示下文中 $$label*(w^Tx+b)$$
     * 定义一个新函数: F(x,y,λ)=f(x,y)+λg(x,y)
     * a为λ（a>=0），代表要引入的拉格朗日乘子(Lagrange multiplier)
-    * 那么:  \\(L(w,b,\alpha)=\frac{1}{2} * ||w||^2 + \sum_{i=1}^{n} \alpha_i * [1 - label * (w^Tx+b)]\\)
-    * 因为: \\(label*(w^Tx+b)>=1, \alpha>=0\\) , 所以 \\(\alpha*[1-label*(w^Tx+b)]<=0\\) , \\(\sum_{i=1}^{n} \alpha_i * [1-label*(w^Tx+b)]<=0\\) 
-    * 当 \\(label*(w^Tx+b)>1\\) 则 \\(\alpha=0\\) ，表示该点为<font color=red>非支持向量</font>
-    * 相当于求解:  \\(max_{关于\alpha} L(w,b,\alpha) = \frac{1}{2} *||w||^2\\) 
-    * 如果求:  \\(min_{关于w, b} \frac{1}{2} *||w||^2\\) , 也就是要求:  \\(min_{关于w, b} \left( max_{关于\alpha} L(w,b,\alpha)\right)\\) 
+    * 那么:  $$L(w,b,\alpha)=\frac{1}{2} * ||w||^2 + \sum_{i=1}^{n} \alpha_i * [1 - label * (w^Tx+b)]$$
+    * 因为: $$label*(w^Tx+b)>=1, \alpha>=0$$ , 所以 $$\alpha*[1-label*(w^Tx+b)]<=0$$ , $$\sum_{i=1}^{n} \alpha_i * [1-label*(w^Tx+b)]<=0$$ 
+    * 当 $$label*(w^Tx+b)>1$$ 则 $$\alpha=0$$ ，表示该点为<font color=red>非支持向量</font>
+    * 相当于求解:  $$max_{关于\alpha} L(w,b,\alpha) = \frac{1}{2} *||w||^2$$ 
+    * 如果求:  $$min_{关于w, b} \frac{1}{2} *||w||^2$$ , 也就是要求:  $$min_{关于w, b} \left( max_{关于\alpha} L(w,b,\alpha)\right)$$ 
 * 现在转化到对偶问题的求解
-    * \\(min_{关于w, b} \left(max_{关于\alpha} L(w,b,\alpha) \right) \\) >= \\(max_{关于\alpha} \left(min_{关于w, b}\ L(w,b,\alpha) \right) \\) 
+    * $$min_{关于w, b} \left(max_{关于\alpha} L(w,b,\alpha) \right) $$ >= $$max_{关于\alpha} \left(min_{关于w, b}\ L(w,b,\alpha) \right) $$ 
     * 现在分2步
-    * 先求:  \\(min_{关于w, b} L(w,b,\alpha)=\frac{1}{2} * ||w||^2 + \sum_{i=1}^{n} \alpha_i * [1 - label * (w^Tx+b)]\\)
+    * 先求:  $$min_{关于w, b} L(w,b,\alpha)=\frac{1}{2} * ||w||^2 + \sum_{i=1}^{n} \alpha_i * [1 - label * (w^Tx+b)]$$
     * 就是求`L(w,b,a)`关于[w, b]的偏导数, 得到`w和b的值`，并化简为: `L和a的方程`。
     * 参考:  如果公式推导还是不懂，也可以参考《统计学习方法》李航-P103<学习的对偶算法>
     ![计算拉格朗日函数的对偶函数](http://data.apachecn.org/img/AiLearning/ml/6.SVM/SVM_5_Lagrangemultiplier.png)
-* 终于得到课本上的公式:  \\(max_{关于\alpha} \left( \sum_{i=1}^{m} \alpha_i - \frac{1}{2} \sum_{i, j=1}^{m} label_i·label_j·\alpha_i·\alpha_j·<x_i, x_j> \right) \\)
-* 约束条件:  \\(a>=0\\) 并且 \\(\sum_{i=1}^{m} a_i·label_i=0\\)
+* 终于得到课本上的公式:  $$max_{关于\alpha} \left( \sum_{i=1}^{m} \alpha_i - \frac{1}{2} \sum_{i, j=1}^{m} label_i·label_j·\alpha_i·\alpha_j·<x_i, x_j> \right) $$
+* 约束条件:  $$a>=0$$ 并且 $$\sum_{i=1}^{m} a_i·label_i=0$$
 
 > 松弛变量(slack variable)
 
@@ -107,13 +107,13 @@ Support Vector Machines: Slide 12 Copyright © 2001, 2003, Andrew W. Moore Why M
 ![松弛变量公式](http://data.apachecn.org/img/AiLearning/ml/6.SVM/SVM_松弛变量.jpg)
 
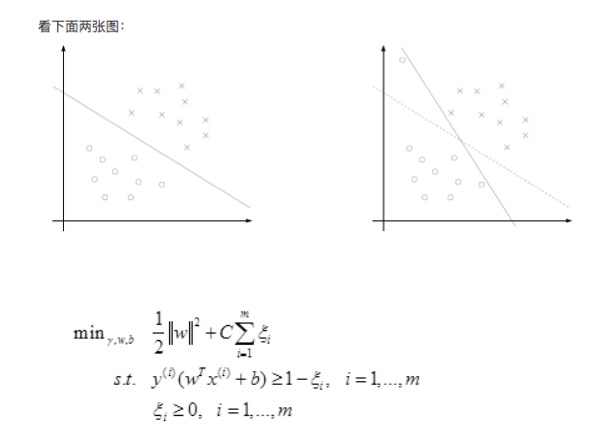
 * 我们知道几乎所有的数据都不那么干净, 通过引入松弛变量来 `允许数据点可以处于分隔面错误的一侧`。
-* 约束条件:  \\(C>=a>=0\\) 并且 \\(\sum_{i=1}^{m} a_i·label_i=0\\)
+* 约束条件:  $$C>=a>=0$$ 并且 $$\sum_{i=1}^{m} a_i·label_i=0$$
 * 总的来说: 
     * ![松弛变量](http://data.apachecn.org/img/AiLearning/ml/6.SVM/松弛变量.png) 表示 `松弛变量`
     * 常量C是 `惩罚因子`, 表示离群点的权重（用于控制“最大化间隔”和“保证大部分点的函数间隔小于1.0” ）
-        * \\(label*(w^Tx+b) > 1\\) and alpha = 0 (在边界外，就是非支持向量)
-        * \\(label*(w^Tx+b) = 1\\) and 0< alpha < C (在分割超平面上，就支持向量)
-        * \\(label*(w^Tx+b) < 1\\) and alpha = C (在分割超平面内，是误差点 -> C表示它该受到的惩罚因子程度)
+        * $$label*(w^Tx+b) > 1$$ and alpha = 0 (在边界外，就是非支持向量)
+        * $$label*(w^Tx+b) = 1$$ and 0< alpha < C (在分割超平面上，就支持向量)
+        * $$label*(w^Tx+b) < 1$$ and alpha = C (在分割超平面内，是误差点 -> C表示它该受到的惩罚因子程度)
         * 参考地址: https://www.zhihu.com/question/48351234/answer/110486455
     * C值越大，表示离群点影响越大，就越容易过度拟合；反之有可能欠拟合。
     * 我们看到，目标函数控制了离群点的数目和程度，使大部分样本点仍然遵守限制条件。
@@ -137,7 +137,7 @@ Support Vector Machines: Slide 12 Copyright © 2001, 2003, Andrew W. Moore Why M
     * 这里指的合适必须要符合一定的条件
         1. 这两个 alpha 必须要在间隔边界之外
         2. 这两个 alpha 还没有进行过区间化处理或者不在边界上。
-    * 之所以要同时改变2个 alpha；原因是我们有一个约束条件:  \\(\sum_{i=1}^{m} a_i·label_i=0\\)；如果只是修改一个 alpha，很可能导致约束条件失效。
+    * 之所以要同时改变2个 alpha；原因是我们有一个约束条件:  $$\sum_{i=1}^{m} a_i·label_i=0$$；如果只是修改一个 alpha，很可能导致约束条件失效。
 
 > SMO 伪代码大致如下: