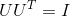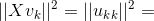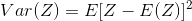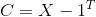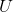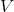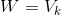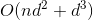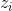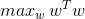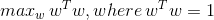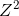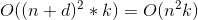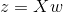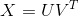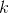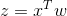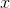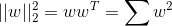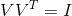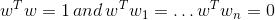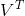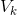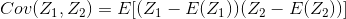ch6 pic
Showing
152 字节
333 字节
247 字节
407 字节
305 字节
580 字节
806 字节
330 字节
146 字节
142 字节
291 字节
500 字节
152 字节
137 字节
432 字节
799 字节
191 字节
840 字节
267 字节
347 字节
133 字节
285 字节
43 字节
124 字节
120 字节
698 字节
293 字节
43 字节
823 字节
186 字节
176 字节
1.3 KB
971 字节
138 字节
298 字节
117 字节