Merge pull request #81 from rickllyxu/dev
校对了Chapter16,翻译了附录CD
Showing
此差异已折叠。
docs/Appendix_C.SVM对偶问题.md
0 → 100644
docs/Appendix_D.自动微分.md
0 → 100644
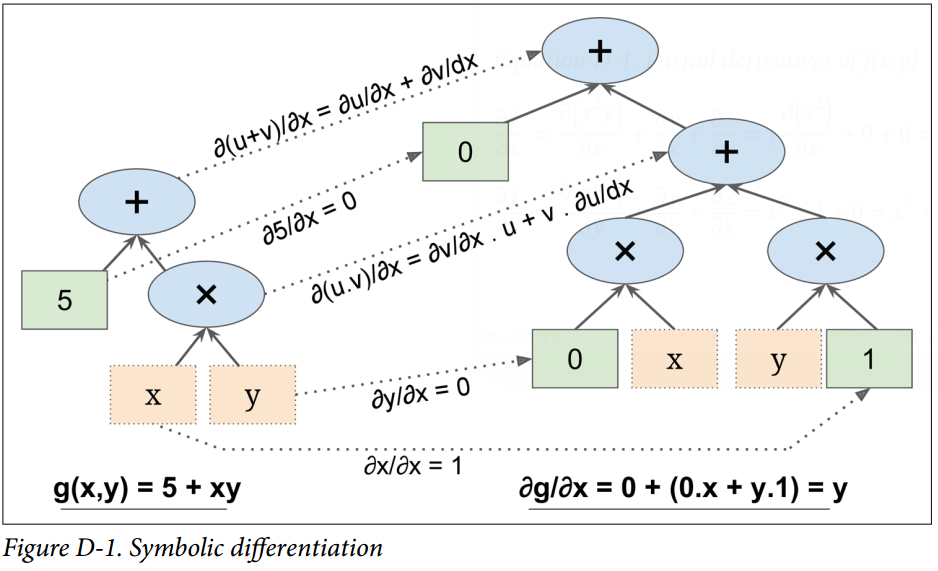
images/Appendix/D-1.png
0 → 100644
160.3 KB
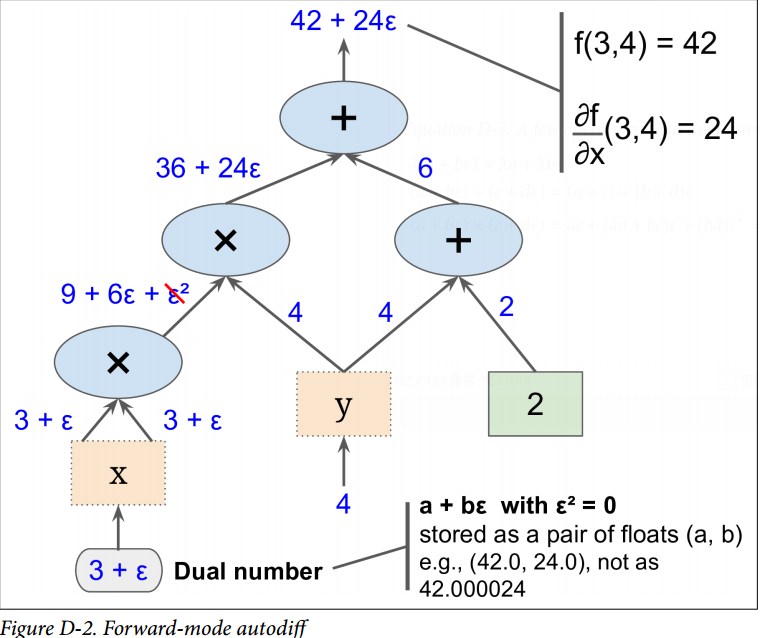
images/Appendix/D-2.png
0 → 100644
123.8 KB
images/Appendix/D-3.png
0 → 100644
132.5 KB
images/Appendix/E_C-1.png
0 → 100644
41.7 KB
images/Appendix/E_C-2.png
0 → 100644
45.5 KB
images/Appendix/E_C-3.png
0 → 100644
29.3 KB
images/Appendix/E_C-4.png
0 → 100644
42.3 KB
images/Appendix/E_C-5.png
0 → 100644
24.1 KB
images/Appendix/E_D-1.png
0 → 100644
41.2 KB
images/Appendix/E_D-2.png
0 → 100644
43.2 KB
images/Appendix/E_D-3.png
0 → 100644
50.7 KB
images/Appendix/E_D-4.png
0 → 100644
8.6 KB
| W: | H:
| W: | H:


| W: | H:
| W: | H:
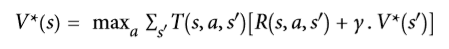
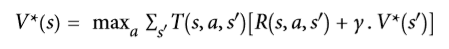
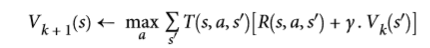
| W: | H:
| W: | H: