Merge pull request #362 from VPrincekin/master
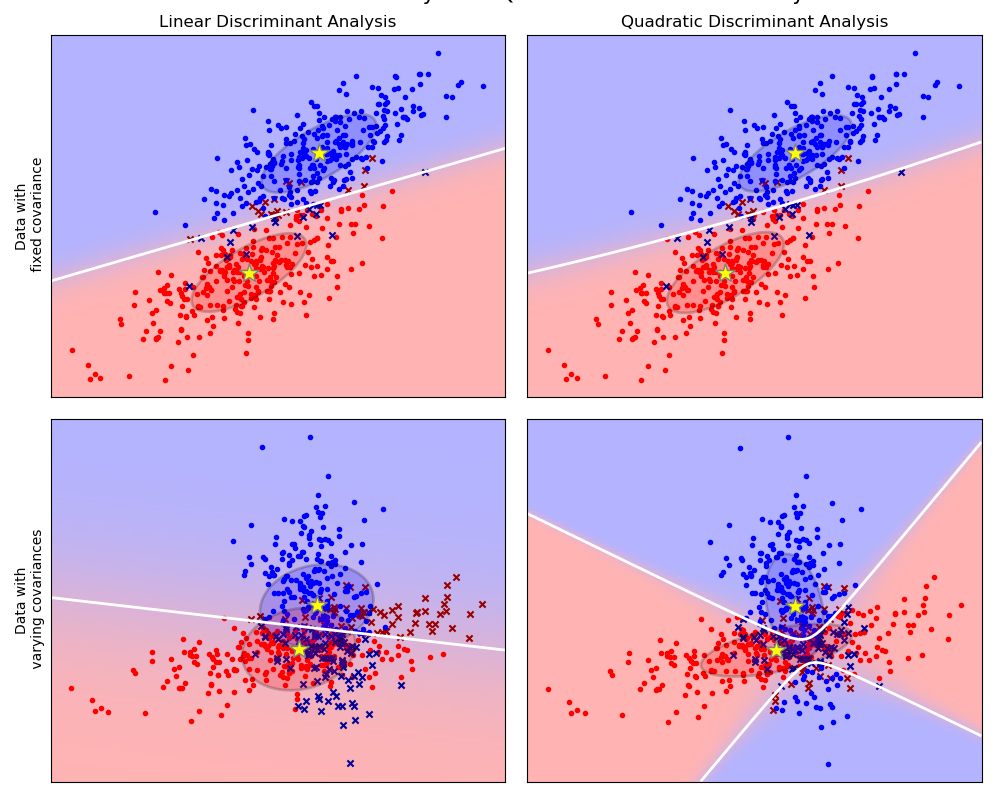
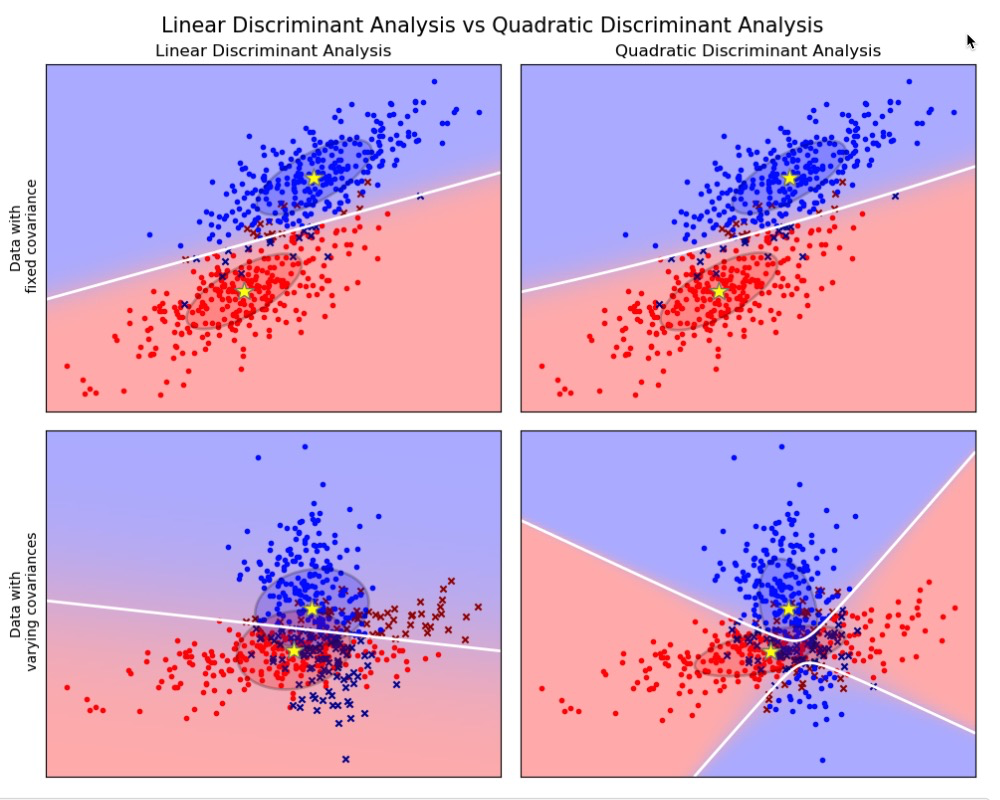
1.2 线性和二次判别分析
Showing

| W: | H:
| W: | H:


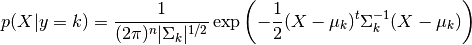
| W: | H:
| W: | H:
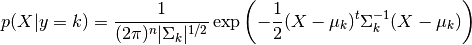
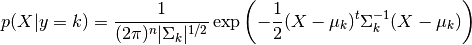
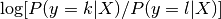
| W: | H:
| W: | H:
| W: | H:
| W: | H:
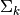
1.7 KB
| W: | H:
| W: | H:


1.2 线性和二次判别分析

2.0 KB | W: | H:
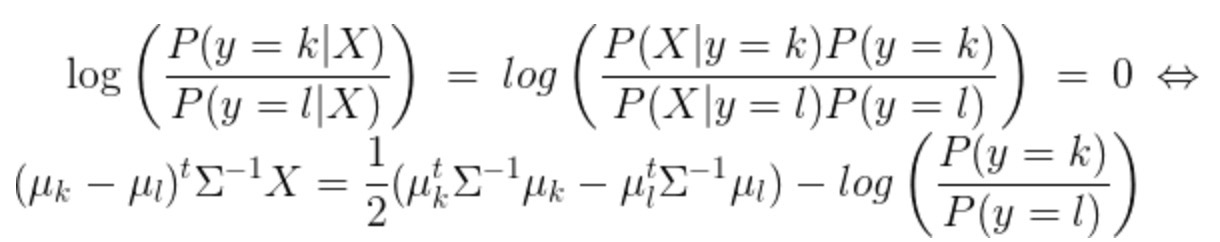
46.2 KB | W: | H:

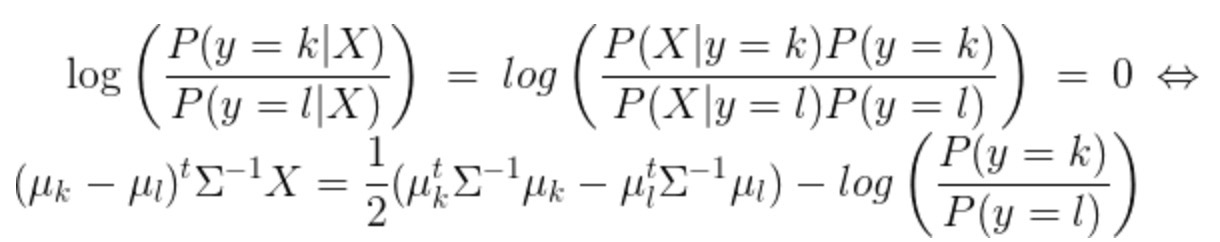

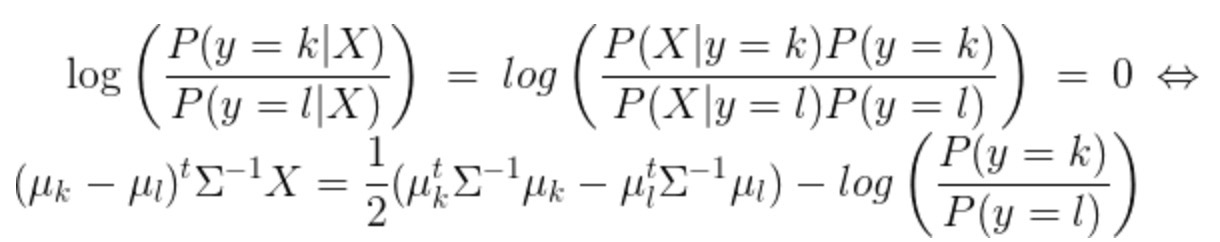
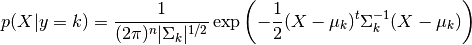
1.9 KB | W: | H:
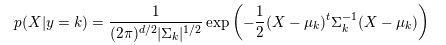
7.2 KB | W: | H:
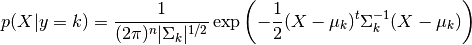
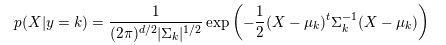
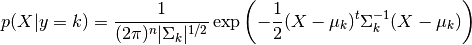
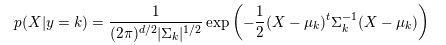
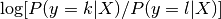
904 字节 | W: | H:
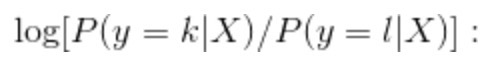
10.4 KB | W: | H:
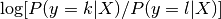
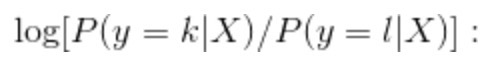
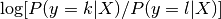
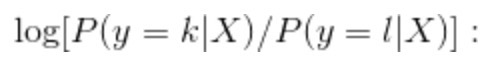
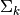
277 字节 | W: | H:
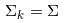
2.0 KB | W: | H:
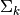
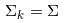
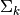
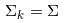
1.7 KB

203.5 KB | W: | H:
610.7 KB | W: | H:




