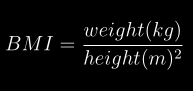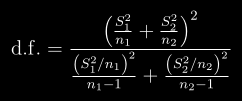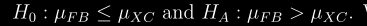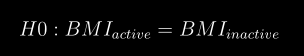update 07.md-09.md
Showing
此差异已折叠。
docs/img/bmi.png
0 → 100644
6.6 KB
docs/img/df.png
0 → 100644
6.9 KB
docs/img/h0-ha.png
0 → 100644
5.1 KB
docs/img/h0.png
0 → 100644
5.0 KB
docs/img/h0coin.png
0 → 100644
4.0 KB
docs/img/h0n.png
0 → 100644
5.4 KB
docs/img/ha.png
0 → 100644
5.3 KB
docs/img/hacoin.png
0 → 100644
4.1 KB
docs/img/han.png
0 → 100644
4.9 KB
docs/img/not-p.png
0 → 100644
3.7 KB
docs/img/poly-distribute.png
0 → 100644
7.1 KB
docs/img/seg.png
0 → 100644
3.0 KB
docs/img/t-student.png
0 → 100644
4.1 KB
docs/img/ufb.png
0 → 100644
5.3 KB