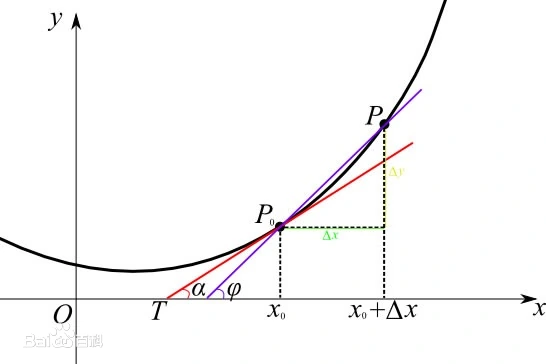
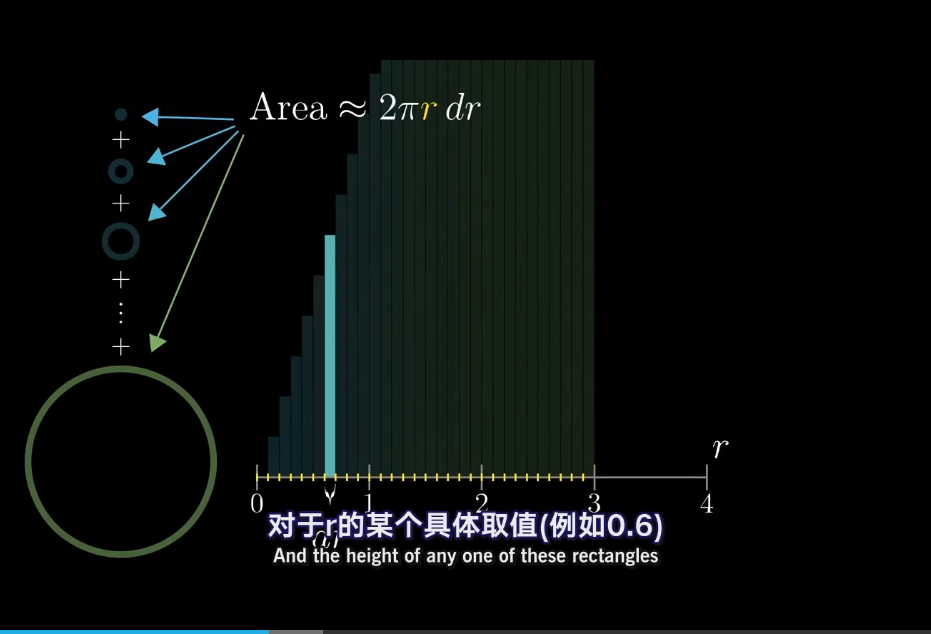
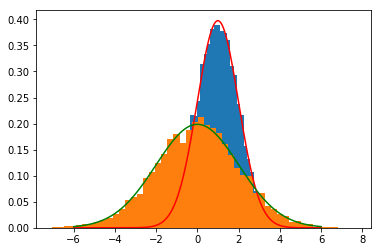
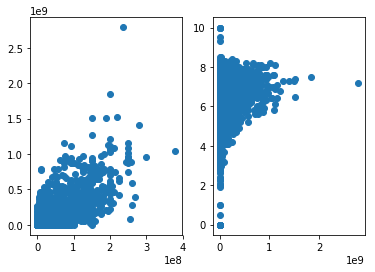
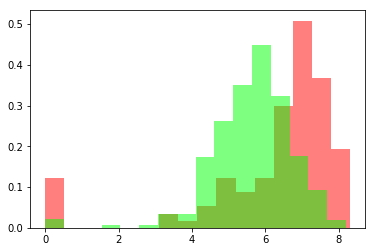
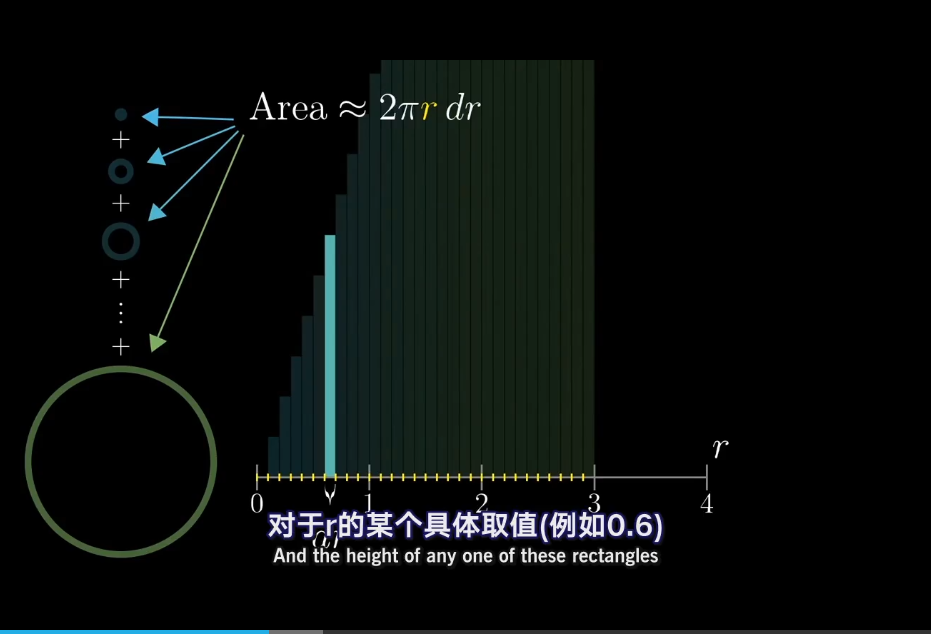
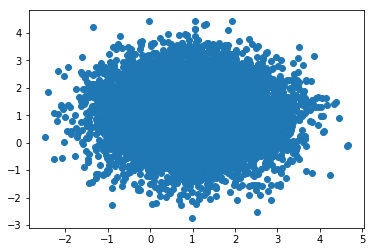
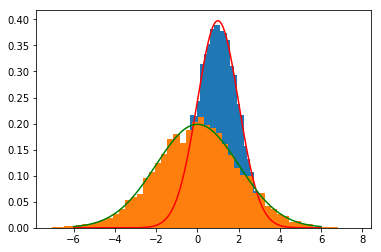
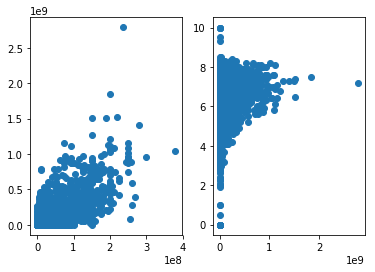
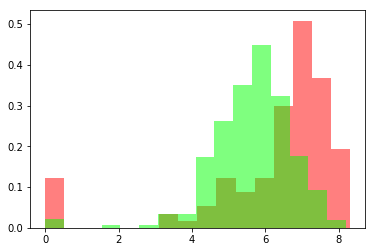
增加函数优化方法笔记

SUMMARY.md

@@ -20,4 +20,6 @@
     * [1.2 科学计算库]
       * [1.2.1 Numpy](numpy.md)
       * [1.2.2 Pandas](pandas.md)
-
+    * [1.3 数学基础]
+      * [1.3.1 微积分基础](calculus.md)
+      * [1.3.1 概率与统计](Probability_Satatistics.md)

book.json

+{
+    "plugins": ["katex"]
+}

example/2.py

+#-*- coding:utf-8 -*-
+import numpy as np
+import matplotlib.pyplot as plt
+import math
+from scipy import stats
+n = 20
+p = 0.3
+k = np.arange(0,41)
+print (k)
+print ("*"*20)
+binomial = stats.binom.pmf(k,n,p)
+print (binomial)
+plt.plot(k, binomial, 'o-')
+plt.title('binomial:n=%i,p=%.2f (www.jb51.net)'%(n,p),fontsize=15)
+plt.xlabel('number of success（脚本之家测试）',fontproperties='SimHei')
+plt.ylabel('probalility of success', fontsize=15)
+plt.grid(True)
+plt.show()
+

example/calculus.py

+import matplotlib.pyplot as plt
+import numpy as np
+
+x= np.arange(-100,100)  # 
+y =  np.pi*x**2
+y1 = 2*np.pi*x
+eta = 10
+while True:
+    x = x + eta
+    y1 = 2*np.pi*x
+    # y = p.tan(2*p.pi*x)
+    plt.plot(x,y,'g-',lw=1)
+    plt.plot(x,y1,'r-',lw=1)
+    # plt.ylim([-4, 4]) # <- Restricting the ylim so we don't see the ~inf values. 
+    plt.show()
\ No newline at end of file

example/contingent_probability.py

+import matplotlib.pyplot as plt
+import numpy as np
+
+def Cov(x1, x2):
+    """
+    协方差，衡量2个变量之间的相关性
+    """
+    return np.mean((x1-np.mean(x1))*(x2-np.mean(x2)))
+
+def rho(x1, x2):
+    """
+    归一化，使2个变量的相关性收敛到0~1之间衡量
+    """
+    return Cov(x1,x2)/(np.std(x1)*np.std(x2))
+
+def N(x, mu, xstd):
+    return 1/(np.sqrt(2*np.pi)*xstd)*np.exp(-(x-mu)**2/(2*xstd**2))
+
+def factorial(a):
+    if a == 0:
+        return 1
+    else:
+        return a*factorial(a-1)
+
+def factorial2(f, n, m):
+    print("n:{0},(f-m+1):{1}".format(n, (f-m+1)))
+    if n == (f-m+1):
+        return (f-m+1)
+    else:
+        return n*factorial2(f, n-1, m)
+
+def B(n, k, p):
+    return factorial2(n, n, k)/factorial(k)*p**k*(1-p)**(n-k)
+
+# x1 = np.random.normal(1.0, 1.0, 100)
+# x2 = np.random.normal(0, 2.0, 100)
+
+x1 = np.random.binomial(1, 0.3, 100)
+x2 = np.random.binomial(1, 0.6, 100)
+# print(x1)
+
+# px1 = len(x1[x1>2])/len(x1)
+# px2 = len(x2[x2>2])/len(x2)
+
+# p = px1*px2
+
+plt.hist(x1, density=True, bins=2)
+plt.hist(x2, density=True, bins=2)
+
+# 创建等差数列
+# xplt = np.linspace(-6, 6, 100)
+# print(xplt)
+
+# # 此处特别注意，输入的xplt是新定义的横轴，mu、std都是输入的随机变量x1,x2
+# xplt1 = N(xplt, np.mean(x1), np.std(x1))
+# xplt2 = N(xplt, np.mean(x2), np.std(x2))
+
+# xplt1 = B(len(x1), len(x1[x1==1]), len(x1[x1==1])/len(x1))
+# xplt2 = B(len(x2), len(x1[x2==1]), len(x2[x2==1])/len(x2))
+
+# # # # print(f"cov(x1,x2):{Cov(x1,x2)}, p1:{px1}, p2:{px2}, p:{p},rho:{rho(x1, x2)}")
+# print(f"cov(x1,x2):{Cov(x1,x2)} ,rho:{rho(x1, x2)}")
+# print(f"xplt1:{xplt1} ,xplt2:{xplt2}")
+
+# plt.scatter(x1, x2)
+# plt.scatter(xplt1, xplt2)
+# plt.plot(xplt, xplt1, color="r")
+# plt.plot(xplt, xplt2, color="g")
+
+plt.show()

example/fuliye.py

+import numpy as np
+import matplotlib.pyplot as plt
+
+x = np.linspace(-np.pi*2, np.pi*2)
+y  = np.sin(x)/np.pi
+y1 = np.sin(3*x)/(np.pi*3)
+y2 = np.sin(5*x)/(np.pi*5)
+y3 = np.sin(7*x)/(np.pi*7)
+y4 = y + y1 + y2 + y3
+
+plt.plot(x, y)
+plt.plot(x, y1)
+plt.plot(x, y2)
+plt.plot(x, y3)
+plt.plot(x, y4)
+
+plt.show()
\ No newline at end of file

example/movie_analyze.py

+import numpy as np
+import matplotlib.pyplot as plt
+import pandas as pd
+
+def Cov(x1, x2):
+    """
+    协方差，衡量2个变量之间的相关性
+    """
+    return np.mean((x1-np.mean(x1))*(x2-np.mean(x2)))
+
+def rho(x1, x2):
+    """
+    归一化，使2个变量的相关性收敛到0~1之间衡量
+    """
+    return Cov(x1,x2)/(np.std(x1)*np.std(x2))
+
+# 需要注意，数据文件需要为utf-8编码，否则会出现索引错乱
+movie_data = pd.read_csv("E:\999_WorkSpace\AI\\aistudynote\example\data\movie.csv")
+# print(movie_data)
+# print(type(movie_data))
+# print(movie_data.columns)
+
+d1 = movie_data["预算"]
+d2 = movie_data["收入"]
+d3 = movie_data["评分"]
+
+# # print(d1)
+# # print(d2)
+
+print(f"cov(d2,d3):{Cov(d2, d3)}, rho(d2,d3):{rho(d2,d3)}")
+
+plt.scatter(d2, d3)
+plt.show()
+
+# score = movie_data["评分"]
+# x1 = movie_data["犯罪"]
+# x2 = movie_data["科幻"]
+
+# # x1==1表示电影类型为犯罪电影，取其索引获取评分
+# score1 = score[x1==1]
+# score2 = score[x2==1]
+
+
+# plt.hist(score1, density=True, color="#FF0000", bins=16, alpha=0.5)
+# plt.hist(score2, density=True, color="#00FF00", bins=16, alpha=0.5)
+# plt.show()

example/multi_var_function_descent.py

+import numpy as np
+import matplotlib.pyplot as plt
+
+def f(x1, x2):
+    return x1**2+2*x1+x2**2+x2
+
+def gradf(x1, x2):
+    gradx1 = 2*x1+2
+    gradx2 = 2*x2+1
+    return gradx1,gradx2
+
+x1, x2 = 1, 1
+y = f(x1, x2)
+
+eta = 0.2
+
+for step in range(1000):
+    gradf1, gradf2 = gradf(x1, x2)
+    x1t = x1 - eta*gradf1
+    x2t = x2 - eta*gradf2
+    yt = f(x1t, x2t)
+    if (yt < y):
+        x1 = x1t
+        x2 = x2t
+        y = yt
+    else:
+        continue
+    print(step, x1, x2, y)
+
+

example/one_var_function_descent.py

+import numpy as np
+import matplotlib.pyplot as plt
+
+def f(x):
+    return x**2 + 2*x + 1
+
+def df(x):
+    return 2*x+1
+
+x = 0
+y = f(x)
+
+# for i in range(1000):
+#     xt = x + np.random.random() - 0.5
+#     yt = f(xt)
+#     if (yt < y):
+#         x = xt
+#         y = yt
+#     else:
+#         continue
+#     print(f"i:{i}, x:{x}, y:{y}")
+
+# xplt = np.linspace(-5, 5, 1000)
+# yplt = f(xplt)
+
+# plt.plot(xplt, yplt)
+# plt.show()
+
+eta = 0.1
+
+for i in range(1000):
+    xt = x - eta*df(x)
+    yt = f(xt)
+    if yt < y:
+        x = xt
+        y = yt
+    else:
+        continue
+    print(f"i:{i}, x:{x}, y:{y}")
\ No newline at end of file

example/stock.py

+import numpy as np
+import matplotlib.pyplot as plt
+import tushare as ts
+
+def model(x1, x2, a, b, c):
+    return a*x1 + b*x2 + c
+
+def gradLoss(x1, x2, a, b, c, d):
+    y = model(x1, x2, a, b, c)
+    dLda = 2*(y-d)*x1
+    dLdb = 2*(y-d)*x2
+    dLdc = 2*(y-d)
+
+    return np.mean(dLda), np.mean(dLdb), np.mean(dLdc)
+
+def floss(x1, x2, a, b, c, d):
+    y = a*x1 + b*x2 + c
+    return np.mean((y-d)**2)
+
+def Cov(x1, x2):
+    """
+    协方差，衡量2个变量之间的相关性
+    """
+    return np.mean((x1-np.mean(x1))*(x2-np.mean(x2)))
+
+def rho(x1, x2):
+    """
+    归一化，使2个变量的相关性收敛到0~1之间衡量
+    """
+    return Cov(x1,x2)/(np.std(x1)*np.std(x2))
+
+# 获得股票数据
+data = ts.get_hist_data("600848")
+
+# 数据预处理
+x = data.values[:, 6]
+x1 = x[:-3]
+x2 = x[1:-2]
+d  = x[2:-1]
+
+# print(x1, x2)
+
+eta = 0.03
+a = 1
+b = 1
+c = 1
+loss = 100
+
+for step in range(10000):
+    ga, gb, gc = gradLoss(x1, x2, a, b, c, d)
+    a -= eta*ga
+    b -= eta*gb
+    c -= eta*gc
+
+    loss_t = floss(x1, x2, a, b, c, d)
+    # print(loss_t, loss)
+    if loss_t < loss:
+        loss = loss_t
+        print(step, a, b, c, loss)
+    else:
+        continue
+
+y1 = model(x1, x2, a, b, c)
+
+print(f"rho(d, y):{rho(d, y1)}")
+
+plt.plot(d, alpha=0.5, color="r", label="Real")
+plt.plot(y1, alpha=0.5, color="g", label="Pre")
+
+plt.legend()
+plt.show()
\ No newline at end of file

homework/homework1.ipynb

+{
+    "cells": [
+        {
+            "cell_type": "markdown",
+            "source": [
+                "#### 1. 统计1~100之和"
+            ],
+            "metadata": {}
+        },
+        {
+            "cell_type": "code",
+            "execution_count": 1,
+            "source": [
+                "import numpy as np\r\n",
+                "\r\n",
+                "sum = 0\r\n",
+                "# 从0开始，到100结束，包含100\r\n",
+                "for i in np.arange(101):\r\n",
+                "    sum += i\r\n",
+                "\r\n",
+                "print(sum)"
+            ],
+            "outputs": [
+                {
+                    "output_type": "stream",
+                    "name": "stdout",
+                    "text": [
+                        "5050\n"
+                    ]
+                }
+            ],
+            "metadata": {}
+        },
+        {
+            "cell_type": "markdown",
+            "source": [
+                "#### 2. 将一个列表的数据复制到另一个列表中"
+            ],
+            "metadata": {}
+        },
+        {
+            "cell_type": "code",
+            "execution_count": 9,
+            "source": [
+                "import copy\r\n",
+                "\r\n",
+                "list1 = np.array([1,2,3,4,5,6])\r\n",
+                "\r\n",
+                "# 浅拷贝\r\n",
+                "list2 = list1\r\n",
+                "list2 = list1[:]\r\n",
+                "\r\n",
+                "print(\"list1 is {}\".format(list1))\r\n",
+                "print(\"list2 is {}\".format(list2))\r\n",
+                "\r\n",
+                "# 修改list1会影响list2\r\n",
+                "list1[2] = 8\r\n",
+                "print(\"list1 id{}, value is {}\".format(id(list1), list1))\r\n",
+                "print(\"list2 is{}, value is {}\".format(id(list2), list2))\r\n",
+                "\r\n",
+                "# 深拷贝\r\n",
+                "list3 = copy.deepcopy(list1)\r\n",
+                "# 修改list1，不会影响list3\r\n",
+                "list1[2] = 10\r\n",
+                "print(\"list1 id{}, value is {}\".format(id(list1), list1))\r\n",
+                "print(\"list3 is{}, value is {}\".format(id(list3), list3))"
+            ],
+            "outputs": [
+                {
+                    "output_type": "stream",
+                    "name": "stdout",
+                    "text": [
+                        "list1 is [1 2 3 4 5 6]\n",
+                        "list2 is [1 2 3 4 5 6]\n",
+                        "list1 id2150405498080, value is [1 2 8 4 5 6]\n",
+                        "list2 is2150405498720, value is [1 2 8 4 5 6]\n",
+                        "list1 id2150405498080, value is [ 1  2 10  4  5  6]\n",
+                        "list3 is2150405497440, value is [1 2 8 4 5 6]\n"
+                    ]
+                }
+            ],
+            "metadata": {}
+        },
+        {
+            "cell_type": "markdown",
+            "source": [
+                "#### 3. 输出9*9乘法口诀表"
+            ],
+            "metadata": {}
+        },
+        {
+            "cell_type": "code",
+            "execution_count": 14,
+            "source": [
+                "import numpy as np\r\n",
+                "\r\n",
+                "for i in range(1,10):\r\n",
+                "    for j in range(1,10):\r\n",
+                "        # print默认输出换行，end参数控制换行符，替换为空格或制表符避免换行\r\n",
+                "        print(\"{0}*{1}={2}\".format(i, j, i*j), end=\"\\t\")\r\n",
+                "        if j == i:\r\n",
+                "            print(\"\")\r\n",
+                "            break"
+            ],
+            "outputs": [
+                {
+                    "output_type": "stream",
+                    "name": "stdout",
+                    "text": [
+                        "1*1=1\t\n",
+                        "2*1=2\t2*2=4\t\n",
+                        "3*1=3\t3*2=6\t3*3=9\t\n",
+                        "4*1=4\t4*2=8\t4*3=12\t4*4=16\t\n",
+                        "5*1=5\t5*2=10\t5*3=15\t5*4=20\t5*5=25\t\n",
+                        "6*1=6\t6*2=12\t6*3=18\t6*4=24\t6*5=30\t6*6=36\t\n",
+                        "7*1=7\t7*2=14\t7*3=21\t7*4=28\t7*5=35\t7*6=42\t7*7=49\t\n",
+                        "8*1=8\t8*2=16\t8*3=24\t8*4=32\t8*5=40\t8*6=48\t8*7=56\t8*8=64\t\n",
+                        "9*1=9\t9*2=18\t9*3=27\t9*4=36\t9*5=45\t9*6=54\t9*7=63\t9*8=72\t9*9=81\t\n"
+                    ]
+                }
+            ],
+            "metadata": {}
+        },
+        {
+            "cell_type": "markdown",
+            "source": [
+                "#### 4. 学习成绩大于等于90；给A，60-89给B；60分以下的给C"
+            ],
+            "metadata": {}
+        },
+        {
+            "cell_type": "code",
+            "execution_count": 22,
+            "source": [
+                "while True:\r\n",
+                "    in_value = input(\"please input your source:\")\r\n",
+                "\r\n",
+                "    if in_value == \"exit\":\r\n",
+                "        break\r\n",
+                "    \r\n",
+                "    print(\"input score is {}\".format(in_value))\r\n",
+                "\r\n",
+                "    try:\r\n",
+                "        score = float(in_value)\r\n",
+                "    except:\r\n",
+                "        print(\"请重新输入正确的分数！\")\r\n",
+                "        continue\r\n",
+                "\r\n",
+                "    if score>= 90.0:\r\n",
+                "        print(\"Your achievement of the course is A\")\r\n",
+                "    elif score>= 60.0:\r\n",
+                "        print(\"Your achievement of the course is B\")\r\n",
+                "    else:\r\n",
+                "        print(\"Your achievement of the course is C\")\r\n",
+                "\r\n",
+                "    "
+            ],
+            "outputs": [
+                {
+                    "output_type": "stream",
+                    "name": "stdout",
+                    "text": [
+                        "input score is 96.36\n",
+                        "Your achievement of the course is A\n"
+                    ]
+                }
+            ],
+            "metadata": {}
+        },
+        {
+            "cell_type": "markdown",
+            "source": [
+                "#### 5. 利用递归的方法求5！"
+            ],
+            "metadata": {}
+        },
+        {
+            "cell_type": "code",
+            "execution_count": 24,
+            "source": [
+                "def factorial(a):\r\n",
+                "    if a == 0:\r\n",
+                "        return 1\r\n",
+                "    else:\r\n",
+                "        return a*factorial(a-1)\r\n",
+                "\r\n",
+                "print(\"factorial(5):{0}\".format(factorial(5)))\r\n",
+                "\r\n",
+                "\r\n"
+            ],
+            "outputs": [
+                {
+                    "output_type": "stream",
+                    "name": "stdout",
+                    "text": [
+                        "factorial(5):120\n"
+                    ]
+                }
+            ],
+            "metadata": {}
+        },
+        {
+            "cell_type": "markdown",
+            "source": [
+                "#### 6. 练习函数的调用：输出三次Hi！"
+            ],
+            "metadata": {}
+        },
+        {
+            "cell_type": "code",
+            "execution_count": null,
+            "source": [
+                "import numpy as np\r\n",
+                "\r\n",
+                "def print_hi():\r\n",
+                "    print(\"Hi\")\r\n",
+                "\r\n",
+                "for i in np.arange(3):\r\n",
+                "    print_hi()"
+            ],
+            "outputs": [],
+            "metadata": {}
+        }
+    ],
+    "metadata": {
+        "orig_nbformat": 4,
+        "language_info": {
+            "name": "python",
+            "version": "3.7.0",
+            "mimetype": "text/x-python",
+            "codemirror_mode": {
+                "name": "ipython",
+                "version": 3
+            },
+            "pygments_lexer": "ipython3",
+            "nbconvert_exporter": "python",
+            "file_extension": ".py"
+        },
+        "kernelspec": {
+            "name": "python3",
+            "display_name": "Python 3.7.0 64-bit ('base': conda)"
+        },
+        "interpreter": {
+            "hash": "d29b27251fa616265523dbf2e992c2aade8e618aaaa8722e8891fc22871ea55d"
+        }
+    },
+    "nbformat": 4,
+    "nbformat_minor": 2
+}
\ No newline at end of file

jupterbotebook/calculus.ipynb

+{
+ "metadata": {
+  "language_info": {
+   "codemirror_mode": {
+    "name": "ipython",
+    "version": 3
+   },
+   "file_extension": ".py",
+   "mimetype": "text/x-python",
+   "name": "python",
+   "nbconvert_exporter": "python",
+   "pygments_lexer": "ipython3",
+   "version": "3.7.0"
+  },
+  "orig_nbformat": 4,
+  "kernelspec": {
+   "name": "python3",
+   "display_name": "Python 3.7.0 64-bit ('base': conda)"
+  },
+  "interpreter": {
+   "hash": "d29b27251fa616265523dbf2e992c2aade8e618aaaa8722e8891fc22871ea55d"
+  }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 2,
+ "cells": [
+  {
+   "source": [
+    "# 微积分的本质\n",
+    "[微积分的本质视频](https://www.bilibili.com/video/BV1qW411N7FU?from=search&seid=8140432043564932117)"
+   ],
+   "cell_type": "markdown",
+   "metadata": {}
+  },
+  {
+   "source": [
+    "# 1. 导数\n",
+    "## 1.1 概念\n",
+    "* 导数就是切线的斜率"
+   ],
+   "cell_type": "markdown",
+   "metadata": {}
+  },
+  {
+   "source": [
+    "# 2. 微分\n",
+    "函数$y = f(x)$在$x$发生极小的变化$\\delta_x$时，函数输出$y$的变化量$\\delta_y$近似于函数的微分$d_y$(近似值),取$d_y$作为函数结果的变化量\n",
+    "\n",
+    "Δy 与 dy"
+   ],
+   "cell_type": "markdown",
+   "metadata": {}
+  },
+  {
+   "source": [
+    "# 3. 积分"
+   ],
+   "cell_type": "markdown",
+   "metadata": {}
+  }
+ ]
+}
\ No newline at end of file

jupterbotebook/probability_satatistics.md

+
+# 1.3.1 概率与统计
+    机器学习从根本上来说是概率与统计方法的延申，二者均是从数据中发现规律并指导生产。
+
+## 1.3.1.1 概念
+* 随机试验
+    观察随机现象所做的试验，产生的事件叫做随机事件
+* 样本空间
+    随机试验中所有可能的结果的集合被称为样本空间
+* 样本点
+    每次试验的结果被称为样本点
+* 统计学与机器学习
+    通过观察分析样本，获得事务规律的过程
+
+## 1.3.1.2 推荐教材
+  * 大学《概率与统计》
+  * 李航《统计学习方法》
+
+## 1.3.1.3 机器学习的过程
+  * 目标：研究掷硬币每个面出现的规律
+  * 设计试验：随机抛，记录每次试验的结果
+  * 样本点：每一次试验的结果
+  * 样本空间：多次试验的结果集合
+  * 统计：分析每个面出现的规律
+  * 机器学习：从数据中发现规律，并指导生产的过程
+
+## 1.3.1.4 机器学习的思路
+    用简单的思路解决复杂的问题
+
+
+```python
+import numpy as np
+import matplotlib.pyplot as plt
+
+coin = np.random.randint(0, 2, 100000)
+coin_arr = np.array(coin)
+# print(coin_arr)
+# print(f"{coin_arr==0, np.sum(coin_arr==0)}")
+print(f"硬币为正面的概率为:{np.sum(coin_arr==0)/len(coin_arr)}")
+
+plt.hist(coin_arr)
+plt.show()
+```
+
+    硬币为正面的概率为:0.50022
+    
+
+
+![png](probability_satatistics_files/probability_satatistics_1_1.png)
+
+
+
+```python
+import numpy as np
+import matplotlib.pyplot as plt
+
+coin = np.random.random(100000)*4
+coin_arr = np.array(coin)
+# print(coin_arr)
+# print(f"{coin_arr==0, np.sum(coin_arr==0)}")
+print(f"硬币为正面的概率为:{np.sum(coin_arr==0)/len(coin_arr)}")
+
+plt.hist(coin_arr, density=True)
+plt.show()
+```
+
+    硬币为正面的概率为:0.0
+    
+
+
+![png](probability_satatistics_files/probability_satatistics_2_1.png)
+
+
+## 1.3.1.5 概率与统计小结
+* 通过对数据进行统计，得到硬币为正面的占比为$\frac{count(0)}{N}$，在样本数量足够大的时候，其概率满足 $p(0)\approx\frac{count(0)}{N}$
+* $p(0)$是一个理想的结果，属于概率论的范畴；
+* $\frac{count(0)}{N}$是对数据的统计，属于统计学范畴
+* 对于离散数据，满足$\sum_{i=1}^{N}p(x_i) = 1$
+* 对于连续数据，仅在积分的情况下才有意义，满足$\int^{+\infty}_{-\infty}p$(x)dx,因为$p(x)dx$才是概率，$p(x)$仅函数是其中$dx$为偏向于0的一个极小的变化量Δx, 概率密度，所以在积分的情况下意义 = 1$
+
+## 1.3.1.6 随机变量的数字特征
+* 平均数
+    假设有三个同学，他们的体重分别为180kg，120kg，100kg，那么他们的平均数是avg = (180+120+100)/3 = 133.33kg
+
+* 加权平均数
+    假设小A去参加歌唱比赛，有3个评委，评委a（专业评委）的打分为9分，其权重为80%，评委b（观众评委）的打分为10分，其权重为15%，评委c（路人评委）的打分为6分，其权重为5%，则其算数平均数为$wavr = (9*0.8+10*0.15+6*0.05)=9$,评分的每个值都有权重。算数平均数的权重可以理解为相等，其数学表达式为$y=f(x)=\sum_{i=1}^{N}w_i*x_i$
+论
+  * 样本均值
+  * 样本方差
+
+* 期望
+在有无穷样本数据情况下的理论均值，根据随机变量分布类型分为离散型随机变量和连续型随机变量。
+* 离散型随机变量的期望公式
+    
+    $$E(x)= \mu(x) =\sum_{i=1}^{\infty}x_i*p_i$$
+    其中$x_i$为第i个随机变量的值，$p_i$为第i个随机变量的值出现的概率,$p_i$就是变量$x_i$的权重
+* 连续型随机变量的期望公式
+
+    $$E(x)= \mu(x) =\int^{+\infty}_{-\infty}x*p(x)dx$$
+    其中$x$为随机变量的值，$p(x)$为随机变量x在偏向于0的极小变化量Δx的概率密度函数，$dx$为自变量Δx，$p(x)*dx$为概率
+    如何理解连续型随机变量的期望公式？
+
+    微积分的理念就是将大的问题分解为小的简单的问题来求解，可以将连续型随机变量分解为有许多Δx(Δx->0)构成,那么可以将连续型随机变量的范围分解为许多宽度为Δx的小的区间，最终求解复杂问题转化为求解概率密度函数p(x)下方的面积的问题，当偏向于0的Δx足够小时，可以每个Δx区间理解为小的矩形，那么其面积为Δx*p(x)；把所有的Δx全部合起来，其面积为x*p(x)*Δx，其数学表示方法即为
+    
+    $$E(x) = \mu(x) = \int^{+\infty}_{-\infty}x*p(x)dx$$
+
+    ![微积分的数学意义](imgs/ex.png)
+
+以上都属于概率论的范畴，也是理想情况，在实际环境中，通过统计学从样本中取得期望，获得期望的无偏估计。
+
+样本均值：
+$$\bar{x} = \frac{\sum_{i=1}^{N}x_i}{N}$$
+
+
+* 方差
+    * 概率论：
+    
+    方差公式：$Var(x)=\sigma^2(x)=\int^{+\infty}_{-\infty}(x-\mu(x))^2*p(x)dx$
+
+    * 统计学：
+    
+    样本方差：$S^2 = \frac{\sum_{i=1}^{N}(x_i-\bar{x})^2}{N-1}$
+* 标准差
+    * 概率论
+    
+    $$\sigma(x)=\sqrt{Var(x)}$$
+    * 统计学
+    
+    样本标准差：
+    $S = \sqrt{\frac{\sum_{i=1}^{N}(x_i-\bar{x})^2}{N-1}}$ 
+    
+
+**机器学习的过程都是对样本进行分析，属于统计学的范畴**
+
+# 1.3.1.6 联合概率分布（多随机变量）
+* 条件概率
+    * 无条件概率
+
+    有一个样本空间Ω，事件A发生的概率为$P(A)=N_A/N_\Omega$
+
+    * 条件概率
+
+    有一个样本空间Ω，事件A发生的概率为P(A)，事件B在事件A发生的时候的概率为P(B|A)，在此处样本空间发生了变化，从Ω变成事件A发生的样本空间$\Omega_A$
+
+    条件概率的定义：已知样本空间$\Omega$,发生A，B两个事件，当$P(B)>0$时，即在事件B发生的条件下事件A也发生的概率,即A对B的条件概率：
+    $$P(A|B) = \frac{P(AB)}{P(B)}$$
+    同理有：
+    $$P(B|A) = \frac{P(AB)}{P(A)}$$
+
+    进行公式变化，则可得，A、B事件同时发生的概率为
+    $$P(AB)  = P(A)P(B|A)$$ 
+
+* 乘法公式
+    $$P(A_1A_2A_3...A_n)=P(A_1)P(A_2|A_1)P(A_3|A_1A_2)...P(A_n|A_1A_2...A_{n-1})$$
+
+以$P(ABC)$推导一下：
+
+AB发生的条件下C发生的概率：
+
+$$P(C|AB)=\frac{P(ABC)}{P(AB)}$$ 
+
+A发生的条件下B发生的概率：
+
+$$P(B|A)=\frac{P(AB)}{P(A)}$$   
+
+则
+$$P(ABC)=P(C|AB)P(AB) = P(C|AB)P(A)P(B|A) = P(A)P(B|A)P(C|AB)$$
+
+* 机器学习
+
+乘法公式
+$$P(ABC)=P(C|AB)P(AB) = P(C|AB)P(A)P(B|A) = P(A)P(B|A)P(C|AB)$$
+也叫概率的分解，多元随机变量的展开
+
+* 全概率公式
+
+![全概率图例](imgs/gailv.png)
+
+事件$A_1$,$A_2$,$A_3$...$A_n$是事件集合E的完备事件组，可以理解为将集合E分为n份，且$有P(A_i)>0$,那么有事件B在集合E中发生的概率为：
+
+$$P(B) = P(A_1B)+P(A_2B)+...+P(A_nB)$$
+$$P(B) = P(A_1)P(B|A_1)+P(A_2)P(B|A_2)+...+P(A_n)P(B|A_n)$$
+
+简写即为
+$$P(B)=\sum_{i=0}^{N}P(A_iB)=\sum_{i=0}^{N}P(A_i)P(B|A_i)$$
+
+连续型随机变量的公式为
+$$P(x1)=\int^{+\infty}_{-\infty}P(x_1x_2)dx_2$$
+在机器学习中，也叫边缘概率
+
+# 1.3.1.7 随机变量的相关性
+用协方差来衡量2个变量之间的相关性，其线性关系表示为
+$$Cov(x_1,x_2)=E((x_1-\mu(x_1)(x_2-\mu(x_2)))$$
+其中$\mu(x_1)$为$x_1$的算数平均数
+
+为了统一衡量标准，对协方差做归一化处理,实现0~1之间来衡量
+$$\rho(x_1,x_2)=\frac{Cov(x_1,x_2)}{\sigma(x_1)\sigma(x_2)}$$
+
+
+```python
+import matplotlib.pyplot as plt
+import numpy as np
+
+def Cov(x1, x2):
+    """
+    协方差，衡量2个变量之间的相关性
+    """
+    return np.mean((x1-np.mean(x1))*(x2-np.mean(x2)))
+
+def rho(x1, x2):
+    """
+    归一化，使2个变量的相关性收敛到0~1之间衡量
+    """
+    return Cov(x1,x2)/(np.std(x1)*np.std(x2))
+
+
+# 高斯分布，低相关性
+x1 = np.random.normal(1.0, 1.0, 10000)
+x2 = np.random.normal(1.0, 1.0, 10000)
+
+px1 = len(x1[x1>2])/len(x1)
+px2 = len(x2[x2>2])/len(x2)
+
+p = px1*px2
+
+print(f"cov(x1,x2):{Cov(x1,x2)}, p1:{px1}, p2:{px2}, p:{p},rho:{rho(x1, x2)}")
+
+plt.scatter(x1, x2)
+plt.show()
+```
+
+    cov(x1,x2):-0.006308131098949094, p1:0.1512, p2:0.1612, p:0.024373440000000003,rho:-0.006370059172326032
+    
+
+
+![png](probability_satatistics_files/probability_satatistics_10_1.png)
+
+
+
+```python
+import matplotlib.pyplot as plt
+import numpy as np
+
+def Cov(x1, x2):
+    """
+    协方差，衡量2个变量之间的相关性
+    """
+    return np.mean((x1-np.mean(x1))*(x2-np.mean(x2)))
+
+def rho(x1, x2):
+    """
+    归一化，使2个变量的相关性收敛到0~1之间衡量
+    """
+    return Cov(x1,x2)/(np.std(x1)*np.std(x2))
+
+
+# 线性关系，高相关性
+x1 = np.random.normal(1.0, 1.0, 10000)
+x2 = x1*2+6
+
+px1 = len(x1[x1>2])/len(x1)
+px2 = len(x2[x2>2])/len(x2)
+
+p = px1*px2
+
+print(f"cov(x1,x2):{Cov(x1,x2)}, p1:{px1}, p2:{px2}, p:{p},rho:{rho(x1, x2)}")
+
+plt.scatter(x1, x2)
+plt.show()
+```
+
+    cov(x1,x2):2.0396521614785774, p1:0.16, p2:0.9983, p:0.159728,rho:1.0
+    
+
+
+![png](probability_satatistics_files/probability_satatistics_11_1.png)
+
+
+# 1.3.1.8 常见数据分布
+* 二项分布
+
+    二项分布,离散型随机变量
+    $$P(k|n)=C_n^kp^k(1-p)^{n-k}$$
+
+    举例：掷n次硬币，有m次正面的概率
+    $$p(x_1,x_2,...,x_n)=p(x_1)p(x_2)...p(x_n)=C_n^mp^m(1-p)^{n-m}$$
+
+* 高斯分布 
+
+    高斯分布,连续型随机变量
+
+    $$p(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{\frac{(x-\mu(x))^2}{2\sigma^2}}$$
+    
+
+
+二项分布展示：
+
+**高斯分布展示**：特别需要注意的是高斯分布输入的x是横轴坐标系，mu和std的输入是随机变量
+
+
+```python
+import matplotlib.pyplot as plt
+import numpy as np
+
+def Cov(x1, x2):
+    """
+    协方差，衡量2个变量之间的相关性
+    """
+    return np.mean((x1-np.mean(x1))*(x2-np.mean(x2)))
+
+def rho(x1, x2):
+    """
+    归一化，使2个变量的相关性收敛到0~1之间衡量
+    """
+    return Cov(x1,x2)/(np.std(x1)*np.std(x2))
+
+def N(x, mu, xstd):
+    return 1/(np.sqrt(2*np.pi)*xstd)*np.exp(-(x-mu)**2/(2*xstd**2))
+
+x1 = np.random.normal(1.0, 1.0, 10000)
+x2 = np.random.normal(0, 2.0, 10000)
+
+# px1 = len(x1[x1>2])/len(x1)
+# px2 = len(x2[x2>2])/len(x2)
+
+# p = px1*px2
+
+plt.hist(x1, density=True, bins=50)
+plt.hist(x2, density=True, bins=50)
+
+# 创建等差数列
+xplt = np.linspace(-6, 6, 10000)
+# print(xplt)
+
+# 此处特别注意，输入的xplt是新定义的横轴，mu、std都是输入的随机变量x1,x2
+xplt1 = N(xplt, np.mean(x1), np.std(x1))
+xplt2 = N(xplt, np.mean(x2), np.std(x2))
+
+# # print(f"cov(x1,x2):{Cov(x1,x2)}, p1:{px1}, p2:{px2}, p:{p},rho:{rho(x1, x2)}")
+print(f"cov(x1,x2):{Cov(x1,x2)} ,rho:{rho(x1, x2)}")
+
+# plt.scatter(x1, x2)
+plt.plot(xplt, xplt1, color="r")
+plt.plot(xplt, xplt2, color="g")
+
+plt.show()
+
+```
+
+    cov(x1,x2):0.015964190908102784 ,rho:0.00791431138835506
+    
+
+
+![png](probability_satatistics_files/probability_satatistics_15_1.png)
+
+
+# 1.3.1.9 常用图例及其作用
+
+* 散点图
+    
+常用来分析两个随机变量的相关性
+
+* 柱状图（直方图）
+
+用用来分析一个随机变量在某个范围内的数据分布
+
+# 1.3.1.10 电影数据分析实战
+* 数据的相关性分析
+    * 电影的票房收入与投入是否存在相关性
+    * 电影的票房收入与评分是否存在相关性
+* 数据分布分析
+    * 哪一类型的电影更容易获得高评分或收入
+
+
+```python
+"""
+数据相关性分析，两个随机变量是否存在相关性。
+"""
+import numpy as np
+import matplotlib.pyplot as plt
+import pandas as pd
+
+def Cov(x1, x2):
+    """
+    协方差，衡量2个变量之间的相关性
+    """
+    return np.mean((x1-np.mean(x1))*(x2-np.mean(x2)))
+
+def rho(x1, x2):
+    """
+    归一化，使2个变量的相关性收敛到0~1之间衡量
+    """
+    return Cov(x1,x2)/(np.std(x1)*np.std(x2))
+
+# 需要注意，数据文件需要为utf-8编码，否则会出现索引错乱
+movie_data = pd.read_csv("E:\999_WorkSpace\AI\\aistudynote\example\data\movie.csv")
+# print(movie_data)
+# print(type(movie_data))
+# print(movie_data.columns)
+
+d1 = movie_data["预算"]
+d2 = movie_data["收入"]
+d3 = movie_data["评分"]
+
+# # print(d1)
+# # print(d2)
+
+# 打印协方差和归一化值
+print(f"cov(d1,d2):{Cov(d1,d2)}, rho(d1,d2):{rho(d1,d2)}")
+print(f"cov(d2,d3):{Cov(d2, d3)}, rho(d2,d3):{rho(d2,d3)}")
+
+# 散点图表现其相关性
+# 预算与收入的相关性展示
+plt.subplot(121)
+plt.scatter(d1, d2)
+
+# 评分与收入的相关性展示
+plt.subplot(122)
+plt.scatter(d2,d3)
+plt.show()
+```
+
+    cov(d1,d2):4845757343880628.0, rho(d1,d2):0.7308228569244815
+    cov(d2,d3):38347693.36660505, rho(d2,d3):0.19714966581131435
+    
+
+
+![png](probability_satatistics_files/probability_satatistics_18_1.png)
+
+
+从上面的图表的左侧图例可知，电影的预算与收入存在较大的相关性，rho值为0.73；电影的收入与评分的相关性较弱，rho值为0.19
+
+
+```python
+"""
+展现同一随机变量【评分】在不同的电影类型下的数据分布，从图标中可知，犯罪电影的评分普遍要比科幻电影高
+"""
+import numpy as np
+import matplotlib.pyplot as plt
+import pandas as pd
+
+def Cov(x1, x2):
+    """
+    协方差，衡量2个变量之间的相关性
+    """
+    return np.mean((x1-np.mean(x1))*(x2-np.mean(x2)))
+
+def rho(x1, x2):
+    """
+    归一化，使2个变量的相关性收敛到0~1之间衡量
+    """
+    return Cov(x1,x2)/(np.std(x1)*np.std(x2))
+
+# 需要注意，数据文件需要为utf-8编码，否则会出现索引错乱
+movie_data = pd.read_csv("E:\999_WorkSpace\AI\\aistudynote\example\data\movie.csv")
+
+score = movie_data["评分"]
+x1 = movie_data["犯罪"]
+x2 = movie_data["科幻"]
+
+# x1==1表示电影类型为犯罪电影，取其索引获取评分
+score1 = score[x1==1]
+score2 = score[x2==1]
+
+plt.hist(score1, density=True, color="#FF0000", bins=16, alpha=0.5)
+plt.hist(score2, density=True, color="#00FF00", bins=16, alpha=0.5)
+plt.show()
+
+```
+
+
+![png](probability_satatistics_files/probability_satatistics_20_0.png)
+
+
+
+```python
+
+```

probability_satatistics.md

+
+# 1.3.1 概率与统计
+
+机器学习从根本上来说是概率与统计方法的延申，二者均是从数据中发现规律并指导生产。
+
+## 1.3.1.1 概念
+
+* 随机试验
+
+观察随机现象所做的试验，产生的事件叫做随机事件
+
+* 样本空间
+
+随机试验中所有可能的结果的集合被称为样本空间
+
+* 样本点
+
+每次试验的结果被称为样本点
+
+* 统计学与机器学习
+
+通过观察分析样本，获得事务规律的过程
+
+
+
+## 1.3.1.2 推荐教材
+
+  * 大学《概率与统计》
+
+  * 李航《统计学习方法》
+
+
+
+## 1.3.1.3 机器学习的过程
+
+  * 目标：研究掷硬币每个面出现的规律
+
+  * 设计试验：随机抛，记录每次试验的结果
+
+  * 样本点：每一次试验的结果
+
+  * 样本空间：多次试验的结果集合
+
+  * 统计：分析每个面出现的规律
+
+  * 机器学习：从数据中发现规律，并指导生产的过程
+
+
+
+## 1.3.1.4 机器学习的思路
+
+用简单的思路解决复杂的问题
+
+
+```python
+import numpy as np
+
+import matplotlib.pyplot as plt
+
+coin = np.random.randint(0, 2, 100000)
+
+coin_arr = np.array(coin)
+
+# print(coin_arr)
+
+# print(f"{coin_arr==0, np.sum(coin_arr==0)}")
+
+print(f"硬币为正面的概率为:{np.sum(coin_arr==0)/len(coin_arr)}")
+
+plt.hist(coin_arr)
+
+plt.show()
+```
+
+硬币为正面的概率为:0.50022
+    
+
+![png](probability_satatistics_files/probability_satatistics_1_1.png)
+
+
+```python
+import numpy as np
+import matplotlib.pyplot as plt
+
+coin = np.random.random(100000)*4
+coin_arr = np.array(coin)
+# print(coin_arr)
+# print(f"{coin_arr==0, np.sum(coin_arr==0)}")
+print(f"硬币为正面的概率为:{np.sum(coin_arr==0)/len(coin_arr)}")
+
+plt.hist(coin_arr, density=True)
+plt.show()
+```
+
+    硬币为正面的概率为:0.0
+    
+
+
+![png](probability_satatistics_files/probability_satatistics_2_1.png)
+
+
+## 1.3.1.5 概率与统计小结
+
+* 通过对数据进行统计，得到硬币为正面的占比为$\frac{count(0)}{N}$，在样本数量足够大的时候，其概率满足 
+
+$$p(0)\approx\frac{count(0)}{N}$$
+
+* $$p(0)$$是一个理想的结果，属于概率论的范畴；
+
+* $$\frac{count(0)}{N}$$是对数据的统计，属于统计学范畴
+
+* 对于离散数据，满足$$\sum_{i=1}^{N}p(x_i) = 1$$
+
+* 对于连续数据，仅在积分的情况下才有意义，满足$\int^{+\infty}_{-\infty}p$(x)dx,因为$p(x)dx$才是概率，$p(x)$仅函数是其中$dx$为偏向于0的一个极小的变化量Δx, 概率密度，所以在积分的情况下意义 = 1$
+
+## 1.3.1.6 随机变量的数字特征
+* 平均数
+    假设有三个同学，他们的体重分别为180kg，120kg，100kg，那么他们的平均数是avg = (180+120+100)/3 = 133.33kg
+
+* 加权平均数
+    假设小A去参加歌唱比赛，有3个评委，评委a（专业评委）的打分为9分，其权重为80%，评委b（观众评委）的打分为10分，其权重为15%，评委c（路人评委）的打分为6分，其权重为5%，则其算数平均数为
+    $$wavr = (9*0.8+10*0.15+6*0.05)=9$$
+    评分的每个值都有权重。算数平均数的权重可以理解为相等，其数学表达式为
+    $$y=f(x)=\sum_{i=1}^{N}w_i*x_i$$
+论
+  * 样本均值
+
+  * 样本方差
+
+* 期望
+在有无穷样本数据情况下的理论均值，根据随机变量分布类型分为离散型随机变量和连续型随机变量。
+* 离散型随机变量的期望公式
+    
+    $$E(x)= \mu(x) =\sum_{i=1}^{\infty}x_i*p_i$$
+    其中$x_i$为第i个随机变量的值，$p_i$为第i个随机变量的值出现的概率,$p_i$就是变量$x_i$的权重
+* 连续型随机变量的期望公式
+
+    $$E(x)= \mu(x) =\int^{+\infty}_{-\infty}x*p(x)dx$$
+    其中$x$为随机变量的值，$p(x)$为随机变量x在偏向于0的极小变化量Δx的概率密度函数，$dx$为自变量Δx，$p(x)*dx$为概率
+    如何理解连续型随机变量的期望公式？
+
+    微积分的理念就是将大的问题分解为小的简单的问题来求解，可以将连续型随机变量分解为有许多Δx(Δx->0)构成,那么可以将连续型随机变量的范围分解为许多宽度为Δx的小的区间，最终求解复杂问题转化为求解概率密度函数p(x)下方的面积的问题，当偏向于0的Δx足够小时，可以每个Δx区间理解为小的矩形，那么其面积为Δx*p(x)；把所有的Δx全部合起来，其面积为x*p(x)*Δx，其数学表示方法即为
+    
+    $$E(x) = \mu(x) = \int^{+\infty}_{-\infty}x*p(x)dx$$
+
+    ![微积分的数学意义](probability_satatistics_files/ex.png)
+
+以上都属于概率论的范畴，也是理想情况，在实际环境中，通过统计学从样本中取得期望，获得期望的无偏估计。
+
+样本均值：
+$$\bar{x} = \frac{\sum_{i=1}^{N}x_i}{N}$$
+
+
+* 方差
+    * 概率论：
+    
+    方差公式：$Var(x)=\sigma^2(x)=\int^{+\infty}_{-\infty}(x-\mu(x))^2*p(x)dx$
+
+    * 统计学：
+    
+    样本方差：$S^2 = \frac{\sum_{i=1}^{N}(x_i-\bar{x})^2}{N-1}$
+* 标准差
+    * 概率论
+    
+    $$\sigma(x)=\sqrt{Var(x)}$$
+    * 统计学
+    
+    样本标准差：
+    $S = \sqrt{\frac{\sum_{i=1}^{N}(x_i-\bar{x})^2}{N-1}}$ 
+    
+
+**机器学习的过程都是对样本进行分析，属于统计学的范畴**
+
+# 1.3.1.6 联合概率分布（多随机变量）
+* 条件概率
+    * 无条件概率
+
+    有一个样本空间Ω，事件A发生的概率为$P(A)=N_A/N_\Omega$
+
+    * 条件概率
+
+    有一个样本空间Ω，事件A发生的概率为P(A)，事件B在事件A发生的时候的概率为P(B|A)，在此处样本空间发生了变化，从Ω变成事件A发生的样本空间$\Omega_A$
+
+    条件概率的定义：已知样本空间$\Omega$,发生A，B两个事件，当$P(B)>0$时，即在事件B发生的条件下事件A也发生的概率,即A对B的条件概率：
+    $$P(A|B) = \frac{P(AB)}{P(B)}$$
+    同理有：
+    $$P(B|A) = \frac{P(AB)}{P(A)}$$
+
+    进行公式变化，则可得，A、B事件同时发生的概率为
+    $$P(AB)  = P(A)P(B|A)$$ 
+
+* 乘法公式
+    $$P(A_1A_2A_3...A_n)=P(A_1)P(A_2|A_1)P(A_3|A_1A_2)...P(A_n|A_1A_2...A_{n-1})$$
+
+以$P(ABC)$推导一下：
+
+AB发生的条件下C发生的概率：
+
+$$P(C|AB)=\frac{P(ABC)}{P(AB)}$$ 
+
+A发生的条件下B发生的概率：
+
+$$P(B|A)=\frac{P(AB)}{P(A)}$$   
+
+则
+$$P(ABC)=P(C|AB)P(AB) = P(C|AB)P(A)P(B|A) = P(A)P(B|A)P(C|AB)$$
+
+* 机器学习
+
+乘法公式
+$$P(ABC)=P(C|AB)P(AB) = P(C|AB)P(A)P(B|A) = P(A)P(B|A)P(C|AB)$$
+也叫概率的分解，多元随机变量的展开
+
+* 全概率公式
+
+![全概率图例](probability_satatistics_files/gailv.png)
+
+事件$A_1$,$A_2$,$A_3$...$A_n$是事件集合E的完备事件组，可以理解为将集合E分为n份，且$有P(A_i)>0$,那么有事件B在集合E中发生的概率为：
+
+$$P(B) = P(A_1B)+P(A_2B)+...+P(A_nB)$$
+$$P(B) = P(A_1)P(B|A_1)+P(A_2)P(B|A_2)+...+P(A_n)P(B|A_n)$$
+
+简写即为
+$$P(B)=\sum_{i=0}^{N}P(A_iB)=\sum_{i=0}^{N}P(A_i)P(B|A_i)$$
+
+连续型随机变量的公式为
+$$P(x1)=\int^{+\infty}_{-\infty}P(x_1x_2)dx_2$$
+在机器学习中，也叫边缘概率
+
+# 1.3.1.7 随机变量的相关性
+用协方差来衡量2个变量之间的相关性，其线性关系表示为
+$$Cov(x_1,x_2)=E((x_1-\mu(x_1)(x_2-\mu(x_2)))$$
+其中$\mu(x_1)$为$x_1$的算数平均数
+
+为了统一衡量标准，对协方差做归一化处理,实现0~1之间来衡量
+$$\rho(x_1,x_2)=\frac{Cov(x_1,x_2)}{\sigma(x_1)\sigma(x_2)}$$
+
+
+```python
+import matplotlib.pyplot as plt
+import numpy as np
+
+def Cov(x1, x2):
+    """
+    协方差，衡量2个变量之间的相关性
+    """
+    return np.mean((x1-np.mean(x1))*(x2-np.mean(x2)))
+
+def rho(x1, x2):
+    """
+    归一化，使2个变量的相关性收敛到0~1之间衡量
+    """
+    return Cov(x1,x2)/(np.std(x1)*np.std(x2))
+
+
+# 高斯分布，低相关性
+x1 = np.random.normal(1.0, 1.0, 10000)
+x2 = np.random.normal(1.0, 1.0, 10000)
+
+px1 = len(x1[x1>2])/len(x1)
+px2 = len(x2[x2>2])/len(x2)
+
+p = px1*px2
+
+print(f"cov(x1,x2):{Cov(x1,x2)}, p1:{px1}, p2:{px2}, p:{p},rho:{rho(x1, x2)}")
+
+plt.scatter(x1, x2)
+plt.show()
+```
+
+    cov(x1,x2):-0.006308131098949094, p1:0.1512, p2:0.1612, p:0.024373440000000003,rho:-0.006370059172326032
+    
+
+
+![png](probability_satatistics_files/probability_satatistics_10_1.png)
+
+
+
+```python
+import matplotlib.pyplot as plt
+import numpy as np
+
+def Cov(x1, x2):
+    """
+    协方差，衡量2个变量之间的相关性
+    """
+    return np.mean((x1-np.mean(x1))*(x2-np.mean(x2)))
+
+def rho(x1, x2):
+    """
+    归一化，使2个变量的相关性收敛到0~1之间衡量
+    """
+    return Cov(x1,x2)/(np.std(x1)*np.std(x2))
+
+
+# 线性关系，高相关性
+x1 = np.random.normal(1.0, 1.0, 10000)
+x2 = x1*2+6
+
+px1 = len(x1[x1>2])/len(x1)
+px2 = len(x2[x2>2])/len(x2)
+
+p = px1*px2
+
+print(f"cov(x1,x2):{Cov(x1,x2)}, p1:{px1}, p2:{px2}, p:{p},rho:{rho(x1, x2)}")
+
+plt.scatter(x1, x2)
+plt.show()
+```
+
+    cov(x1,x2):2.0396521614785774, p1:0.16, p2:0.9983, p:0.159728,rho:1.0
+    
+
+
+![png](probability_satatistics_files/probability_satatistics_11_1.png)
+
+
+# 1.3.1.8 常见数据分布
+* 二项分布
+
+    二项分布,离散型随机变量
+    $$P(k|n)=C_n^kp^k(1-p)^{n-k}$$
+
+    举例：掷n次硬币，有m次正面的概率
+    $$p(x_1,x_2,...,x_n)=p(x_1)p(x_2)...p(x_n)=C_n^mp^m(1-p)^{n-m}$$
+
+* 高斯分布 
+
+    高斯分布,连续型随机变量
+
+    $$p(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{\frac{(x-\mu(x))^2}{2\sigma^2}}$$
+    
+
+
+二项分布展示：
+
+**高斯分布展示**：特别需要注意的是高斯分布输入的x是横轴坐标系，mu和std的输入是随机变量
+
+
+```python
+import matplotlib.pyplot as plt
+import numpy as np
+
+def Cov(x1, x2):
+    """
+    协方差，衡量2个变量之间的相关性
+    """
+    return np.mean((x1-np.mean(x1))*(x2-np.mean(x2)))
+
+def rho(x1, x2):
+    """
+    归一化，使2个变量的相关性收敛到0~1之间衡量
+    """
+    return Cov(x1,x2)/(np.std(x1)*np.std(x2))
+
+def N(x, mu, xstd):
+    return 1/(np.sqrt(2*np.pi)*xstd)*np.exp(-(x-mu)**2/(2*xstd**2))
+
+x1 = np.random.normal(1.0, 1.0, 10000)
+x2 = np.random.normal(0, 2.0, 10000)
+
+# px1 = len(x1[x1>2])/len(x1)
+# px2 = len(x2[x2>2])/len(x2)
+
+# p = px1*px2
+
+plt.hist(x1, density=True, bins=50)
+plt.hist(x2, density=True, bins=50)
+
+# 创建等差数列
+xplt = np.linspace(-6, 6, 10000)
+# print(xplt)
+
+# 此处特别注意，输入的xplt是新定义的横轴，mu、std都是输入的随机变量x1,x2
+xplt1 = N(xplt, np.mean(x1), np.std(x1))
+xplt2 = N(xplt, np.mean(x2), np.std(x2))
+
+# # print(f"cov(x1,x2):{Cov(x1,x2)}, p1:{px1}, p2:{px2}, p:{p},rho:{rho(x1, x2)}")
+print(f"cov(x1,x2):{Cov(x1,x2)} ,rho:{rho(x1, x2)}")
+
+# plt.scatter(x1, x2)
+plt.plot(xplt, xplt1, color="r")
+plt.plot(xplt, xplt2, color="g")
+
+plt.show()
+
+```
+
+    cov(x1,x2):0.015964190908102784 ,rho:0.00791431138835506
+    
+
+
+![png](probability_satatistics_files/probability_satatistics_15_1.png)
+
+
+# 1.3.1.9 常用图例及其作用
+
+* 散点图
+    
+常用来分析两个随机变量的相关性
+
+* 柱状图（直方图）
+
+用用来分析一个随机变量在某个范围内的数据分布
+
+# 1.3.1.10 电影数据分析实战
+* 数据的相关性分析
+    * 电影的票房收入与投入是否存在相关性
+    * 电影的票房收入与评分是否存在相关性
+* 数据分布分析
+    * 哪一类型的电影更容易获得高评分或收入
+
+
+```python
+"""
+数据相关性分析，两个随机变量是否存在相关性。
+"""
+import numpy as np
+import matplotlib.pyplot as plt
+import pandas as pd
+
+def Cov(x1, x2):
+    """
+    协方差，衡量2个变量之间的相关性
+    """
+    return np.mean((x1-np.mean(x1))*(x2-np.mean(x2)))
+
+def rho(x1, x2):
+    """
+    归一化，使2个变量的相关性收敛到0~1之间衡量
+    """
+    return Cov(x1,x2)/(np.std(x1)*np.std(x2))
+
+# 需要注意，数据文件需要为utf-8编码，否则会出现索引错乱
+movie_data = pd.read_csv("E:\999_WorkSpace\AI\\aistudynote\example\data\movie.csv")
+# print(movie_data)
+# print(type(movie_data))
+# print(movie_data.columns)
+
+d1 = movie_data["预算"]
+d2 = movie_data["收入"]
+d3 = movie_data["评分"]
+
+# # print(d1)
+# # print(d2)
+
+# 打印协方差和归一化值
+print(f"cov(d1,d2):{Cov(d1,d2)}, rho(d1,d2):{rho(d1,d2)}")
+print(f"cov(d2,d3):{Cov(d2, d3)}, rho(d2,d3):{rho(d2,d3)}")
+
+# 散点图表现其相关性
+# 预算与收入的相关性展示
+plt.subplot(121)
+plt.scatter(d1, d2)
+
+# 评分与收入的相关性展示
+plt.subplot(122)
+plt.scatter(d2,d3)
+plt.show()
+```
+
+    cov(d1,d2):4845757343880628.0, rho(d1,d2):0.7308228569244815
+    cov(d2,d3):38347693.36660505, rho(d2,d3):0.19714966581131435
+    
+
+
+![png](probability_satatistics_files/probability_satatistics_18_1.png)
+
+
+从上面的图表的左侧图例可知，电影的预算与收入存在较大的相关性，rho值为0.73；电影的收入与评分的相关性较弱，rho值为0.19
+
+
+```python
+"""
+展现同一随机变量【评分】在不同的电影类型下的数据分布，从图标中可知，犯罪电影的评分普遍要比科幻电影高
+"""
+import numpy as np
+import matplotlib.pyplot as plt
+import pandas as pd
+
+def Cov(x1, x2):
+    """
+    协方差，衡量2个变量之间的相关性
+    """
+    return np.mean((x1-np.mean(x1))*(x2-np.mean(x2)))
+
+def rho(x1, x2):
+    """
+    归一化，使2个变量的相关性收敛到0~1之间衡量
+    """
+    return Cov(x1,x2)/(np.std(x1)*np.std(x2))
+
+# 需要注意，数据文件需要为utf-8编码，否则会出现索引错乱
+movie_data = pd.read_csv("E:\999_WorkSpace\AI\\aistudynote\example\data\movie.csv")
+
+score = movie_data["评分"]
+x1 = movie_data["犯罪"]
+x2 = movie_data["科幻"]
+
+# x1==1表示电影类型为犯罪电影，取其索引获取评分
+score1 = score[x1==1]
+score2 = score[x2==1]
+
+plt.hist(score1, density=True, color="#FF0000", bins=16, alpha=0.5)
+plt.hist(score2, density=True, color="#00FF00", bins=16, alpha=0.5)
+plt.show()
+
+```
+
+
+![png](probability_satatistics_files/probability_satatistics_20_0.png)
+
+
+
+```python
+
+```

probability_satatistics.md.bak

+#### 1.3.1 概率与统计
+    机器学习从根本上来说是概率与统计方法的延申，二者均是从数据中发现规律并指导生产。
+
+##### 1.3.1.1 概念
+* 随机试验
+    观察随机现象所做的试验，产生的事件叫做随机事件
+* 样本空间
+    随机试验中所有可能的结果的集合被称为样本空间
+* 样本点
+    每次试验的结果被称为样本点
+* 统计学与机器学习
+    通过观察分析样本，获得事务规律的过程
+
+* 推荐教材
+  * 大学《概率与统计》
+  * 李航《统计学习方法》
+
+* 机器学习的过程
+  * 目标：研究掷硬币每个面出现的规律
+  * 设计试验：随机抛，记录每次试验的结果
+  * 样本点：每一次试验的结果
+  * 样本空间：多次试验的结果集合
+  * 统计：分析每个面出现的规律
+  * 机器学习：从数据中发现规律，并指导生产的过程
+
+* 机器学习的思路
+    用简单的思路解决复杂的问题
+
+* 代码实现示例
+
+```
+import numpy as np
+import matplotlib.pyplot as plt
+
+coin = np.random.randint(0, 2, 100000)
+coin_arr = np.array(coin)
+# print(coin_arr)
+# print(f"{coin_arr==0, np.sum(coin_arr==0)}")
+print(f"硬币为正面的概率为:{np.sum(coin_arr==0)/len(coin_arr)}")
+
+plt.hist(coin_arr)
+plt.show()
+```
+
+* 概率与统计小结
+    * 通过对数据进行统计，得到硬币为正面的占比为$$\frac{count(0)}{N}$$，在样本数量足够大的时候，其概率满足 
+        $$p(0)\approx\frac{count(0)}{N}$$
+
+    * $$p(0)$$是一个理想的结果，属于概率论的范畴；
+    * $$\frac{count(0)}{N}$$是对数据的统计，属于统计学范畴
+    * 对于离散数据，满足
+        $$\sum_{i=1}^{Nn}p(x_i) = 1$$ 
+    * 对于连续数据，仅在积分的情况下才有意义，满足
+        $$\int^{+\infty}_{-\infty}p(x)dx = 1$$
+
+##### 1.3.1.2 连续数据与离散散点数据
+* 连续数据
+
+```
+import numpy as np
+import matplotlib.pyplot as plt
+
+# 生成指定数量的0~1之间的随机数
+x1 = np.random.random(1000000)
+x2 = np.random.random(1000000)*5
+plt.hist(x1, bins=36, density=True)
+plt.hist(x2, bins=36, density=True)
+plt.show()
+```
+
+对于连续数据，概率仅在积分的情况下才有意义，为啥呢？
+
+
+
+

python_base/homework.md

+### 1. 作业规范
+* 说明报告PDF文件，包含文字和代码，结论
+* 可执行python文件或jupter notebook文件
+* 正课：数据保存到网盘，附上链接
+
+### 2. python基础作业
+#### 2.1 统计1~100之后
+#### 2.2 将一个列表的数据复制到另一个列表中
+#### 2.3 输出9*9乘法口诀表
+#### 2.4 学习成绩大于等于90；给A，60-89给B；60分以下的给C
+#### 2.5 利用递归的方法求5！
+#### 2.6 练习函数的调用：输出三次Hi！
+
+